El método más intuitivo para saber cúal es el mínimo común múltiplo de varios números, consiste en calcular los múltiplos de cada número y, el menor múltiplo común a dichos números será su Mínimo Común Múltiplo.
Ejemplo:
Calculamos el Mínimo Común Múltiplo de 6, 12 y 18
El menor múltiplo común a los tres números es 36
Por lo que el m.c.m. (6 , 12 , 18) = 36.
- Los múltiplos de 6 son ⇒ 6, 12, 18, 24, 30, 36 ...
- Los múltiplos de 12 son ⇒ 12, 24, 36, 48, 60 ...
- Los múltiplos de 18 son ⇒ 18, 36, 54, 72, 90 ...
El menor múltiplo común a los tres números es 36
Por lo que el m.c.m. (6 , 12 , 18) = 36.
Este método no nos sirve para números grandes ya que el procedimiento de calcular multiplos de los números se hace complicado para encontrar el común.
Otro procedimiento para calcular el mínimo común múltiplo, más corto y que resulta más fácil de utilizar es seguir los siguientes pasos:
- Descomponer en un producto de factores primos los números los números.
- Tomamos todos los factores UNA vez el que este elevado al mayor exponente.
- El m.c.m. es el producto de los factores anteriores. Ejemplo: calcular el MCD de 24, 36 y 40. 1. Descomponer en un producto de factores primos los números los números
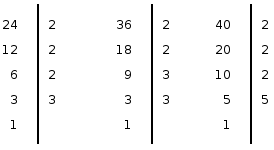

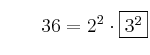
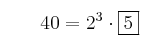
2. Los factores son: 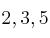 y elvados a los mayores exponentes serían:
y elvados a los mayores exponentes serían: 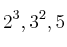 .
.
3. Multiplicando los factores anteriores se obtiene el mcm
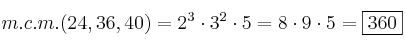
Máximo Común Divisor.
El Máximo Común Divisor (M.C.D. o MCD) de varios números es el mayor de sus divisores comunes.
Pasos para calcularlo:
1. Descomponemos en un producto de factores primos los números

2. Tomamos todos los factores comunes elevados a los menores exponentes.
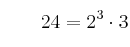
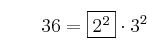
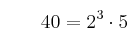
3. El M.C.D. es el producto de los factores anteriores.
Factores comunes a todos los números es el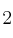 , y elevado al menor exponente sería:
, y elevado al menor exponente sería: 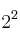 .
.
Por tanto:
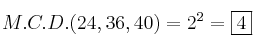
3. Multiplicando los factores anteriores se obtiene el mcm
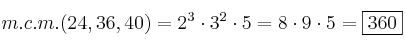
Máximo Común Divisor.
El Máximo Común Divisor (M.C.D. o MCD) de varios números es el mayor de sus divisores comunes.
Pasos para calcularlo:
- Descomponemos en un producto de factores primos los números
- Tomamos todos los factores comunes elevados a los menores exponentes
- El M.C.D. es el producto de los factores anteriores
1. Descomponemos en un producto de factores primos los números

2. Tomamos todos los factores comunes elevados a los menores exponentes.
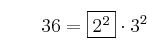
3. El M.C.D. es el producto de los factores anteriores.
Factores comunes a todos los números es el
Por tanto:
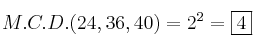
De todo.
http://www.aprendermatematicas.com/libro_nuevo/02_divisibilidad/libro_divisibilidad.swf
http://bibliojcalde.zz.mu/genmagic/multiplos_divisores.swf
Multiplos de un número.
http://bibliojcalde.zz.mu/genmagic/multiplos_numero.swfhttp://bibliojcalde.zz.mu/genmagic/multiplos_numero.swf
M.c.m.
http://bibliojcalde.zz.mu/flash/mates/minimo_c_multiplo.swfhttp://bibliojcalde.zz.mu/flash/mates/minimo_c_multiplo.swf
http://bibliojcalde.zz.mu/flash/mates/minimo_c_multiplo_tanque.swf
No hay comentarios:
Publicar un comentario